Introduction

 

UNEVEN AGED MANAGEMENT, the cutting of a few stems from a stand of trees of different species and size, while leaving others to grow and replace them, is the oldest form of forest management. Instead, even-aged management, the production of monospecific trees of same size starting from bare land, came much later in parallel with the development of intensive agriculture. When our forebears went into the forest to choose the perfect cedar tree to make a dugout canoe, they were doing what we call a "selection cut," though they were probably not much concerned about regeneration, because good trees were plentiful. Later, when villages grew into nations, and canoes into fleets of mighty timbered vessels, regeneration did become a problem, and elaborate rules had to be set on how many and how big the trees that could be taken, and when. Then, full fledged unevenaged silvicultural systems came of age. Still, uneven-aged systems are the exception rather than the norm in current silviculture. They have survived in special settings and for specific purposes, especially in mountainous areas where maintaining a continuous forest cover was essential to control erosion.

Today, there is a interest in multi-species uneven-aged forests, in which the number of trees diminishes steadily with increasing stem diameter (Daniel et al. 1979). They are eminently suited to the multiple purposes of modern forests, as fonts of biodiversity, as aesthetic environment, for soil conservation, and, not least for economic timber production. In particular, uneven-aged stands with trees of many species and sizes are inherently very diverse. As a result, they are pleasing aesthetically and spiritually. Ammer (1994) found that "what visitors enjoy is to see several generations of trees growing together in a forest managed under a selective system. They are moved by the harmony of such a structure which brings all age groups together in a very small area (the "father-mother-child" pattern)."

This undeniably romantic appeal of uneven-aged forests, coupled with their real and presumed ability to nurture biological diversity, is giving them a central place in contemporary forestry. In the United States, uneven-aged forests form the core element of the "ecosystem management" philosophy for national forests. In Europe, they are at the center of the theories and practices of the "nature oriented silviculture" (Ciancio and Nocentini 1994).

Unfortunately, there is still little scientific information to support this extended use of uneven-aged management. We need to know much more about the growth of uneven-aged forests and how they are affected by management. I will report on some methods to predict such developments. The examples are those that I know best, derived from studies in Europe and North America. It should be clear however that this work stems from and is tied to the work of many others. I will begin with a brief descriptions of forests I have used as case studies, in Wisconsin, the Southern United States, France and Italy. I will then proceed to describe the methods that have resulted from this work: growth models to mimic the life cycle of trees, simulation to predict the effects of different managements, and optimization to seek the best management for a given set of objectives.

Uneven-Aged Forests

The northern hardwoods

IN THE NORTH-EAST AND NORTH-CENTRAL United States, one of the most extensive types is the maple-basswood-birch forest (also called the northern hardwoods, or maple-birch type). In Wisconsin it covers nearly one third of the state forest area. This forest is in large part second-growth, a result of the extensive logging and clearing that took place at the turn of the century. The famous Wisconsin pineries were then entirely cut over, making a few people immensely rich, and providing capital and materials to build the western towns and railroads. The policy, then, was to change the forests into farms. But a harsh climate and poor soils did not allow this. Most farms in Northern Wisconsin were abandoned, and the land reverted to forest.

Despite past indiscriminate logging, the beauty of the northern forest has returned, most strikingly in the fall with the varied colors of its maples and birches. It is a haven for a very diverse wildlife, birds, and fauna. Meanwhile, the Wisconsin forest has a major economic role as the source of raw material for an active industry. In particular, Wisconsin is the largest producing state for pulp and paper, both in tonnage and value. Three fourths of the Wisconsin forest is privately owned, and Bliss and Martin (1988) have found that the owners have varied objectives. It is therefore essential to develop silvicultural techniques for multiple use on the smallest tracts of land. Uneven-aged systems seem especially well suited for this forest type. The avoidance of clear cutting protects the amenity values of the maple-birch forest, while natural regeneration enhances economic returns.

Because they are typical examples of uneven-aged forests, northern hardwoods have served as cases in much modeling work in North America. Several papers have reported on the ecological and economic implications of uneven-aged management of mixed northern hardwood forests (Adams and Ek 1974, Buongiorno and Michie 1980, Haight 1985, Bare and Opalach 1987), and a few have dealt with some ecological implications (Lu and Buongiorno 1993, Buongiorno et al. 1994, Niese and Strong 1992).

 

The southern pine-hardwood forests

FORESTRY IS ALSO IMPORTANT in the economy of the southeastern United States. The region contains over 211 million acres of forest land, mostly private. A quarter of private holdings are held by forest industry, while federal holdings cover about 12 million acres. Loblolly pine and shortleaf pine cover 50 million acres and comprise over two-thirds of the region's merchantable timber (Powell et al. 1993).

Loblolly pine, the primary commercial species in the region, is generally managed with even-aged silviculture: clear cut followed by site preparation and planting. This approach provides profitable returns for industry and individual owners. But, this is at the expense of ecological diversity at the stand level, although even-aged stands can contribute to the diversity of a forest landscape.

Growing awareness of the importance of maintaining an ecologically diverse mix of species and size classes has heightened interest in alternatives to even-aged, single-species regimes. Fortunately, the Forest Inventory and Analysis data base has a large number of plots, throughout the southeastern regions, that have a typical uneven-aged structure (inverse J shape tree diameter distribution), natural regeneration, and a mix of pines, soft hardwoods and hard hardwoods. As we will see below, such data can be used to predict the results of uneven-aged management in the loblolly pine forest type.

Studies of uneven-aged management of southern pines have addressed the determination of effective stand structures (number of trees in each size class) and cutting cycles (interval between harvests) for high timber production. Usually, the management criteria have been the present value of the returns or the volume of timber produced per unit time, over a short time horizon (e.g., Hotvedt et al. 1989, Farrar 1981, Williston 1978). Murphy and Shelton (1994) have initiated loblolly pine uneven-aged stand growth modeling, while Guldin and Baker (1988) have compared yields between even-aged and uneven-aged loblolly-shortleaf pine stands. Lin and others (1996b), have begun to develop models with explicit measures of tree species and size in loblolly pine stands.

 

Mountain forests in the French Jura

IN CONTRAST TO NORTH AMERICA, uneven-aged management has had a long history in Europe. In the Jura mountains of France, the "futaie jardinee," was recognized as a system of silviculture by the State administration as early as 1730. Still, the "jardinage" was fought against, especially after 1830, by tenants of more Cartesian even-aged systems. It took the revolt led by Gurnaud in 1880 to force the acceptance of uneven-aged techniques, like the "methode du controle" as proper silviculture for the fir and spruce forests in mountains (Gurnaud, 1886).

Since then, uneven-aged management has been a common practice in the French Jura and neighboring Switzerland. But few formal tools are available to guide it. Until 1950, the application of common norms (e.g. Schaeffer et al. 1930) appears to have led to stands with too much basal area, which hampered regeneration and led to old even-aged stands. Current policies are trying to rejuvenate them by cutting enough trees to insure continuous regeneration.

In the Jura uneven-aged silviculture is attractive, because it keeps a natural look to the forest, with a mix of firs, spruces, and beeches of various sizes on the same area. It also protects the soil against erosion by maintaining a continuous forest cover. Moreover, it is economical because natural regeneration is free, while it gives high-value products. Technically, it is judged more difficult to implement because it requires the marking of individual trees by skilled foresters, though simple guidelines could facilitate the marking operation.

The uneven-aged forests of the Jura are among the richest in France. They always have contributed substantially to the welfare of local communities. Therefore, the economic function of these forests is important, and it is likely to remain so. However, there, like in many other countries, biodiversity is becoming an ever more important goal of forest management. Uneven-aged silviculture has a privileged role in this context, at levels that go from the entire landscape and biome, to limited micro sites.

 

Forests of the Italian Alps

IN ITALY, WE HAVE STUDIED the mixed stands of spruce, fir, beech, and larch in the public forests in the central-eastern Alps and Prealps of the Veneto Region. These forests have been managed for centuries, in particular by the Serenissima Repubblica di Venezia. Selective cutting was imposed by Venice to provide good timber for building a powerful military and commercial fleet, without exhausting the forest and compromising its natural regeneration. In this system, most of the largest trees were cut, plus those in smaller size classes which were damaged or out competed. A common diameter limit was 60 to 70 cm for conifers, somewhat lower for broad-leaved species.

The silvicultural policies introduced by the Republic of Venice assured self regeneration and long-term production. The legislation of the Republic of Venice in matters of silviculture was wide ranging and still underlies forest management principles in the Italian Alps. Today the selective cut silviculture is still favored in the public forests of the Italian Alps. Clear cuts are not allowed, not even in private forests, though intermediate forms of treatments between uneven-aged management and shelterwood may be applied.

The forests in the Italian Dolomites and Trentino are among the most productive in the southern Alps, they are also part of a beautiful landscape with preferred areas for hiking, skiing, and enjoying nature. Nevertheless, foresters are facing difficult problems. First, a weakness of the forest structure, due to reduction of its complexity, both in terms of number of tree species and size distribution. Second, like in the French Jura, many stands are not self-regenerating, for reasons

that are not completely understood. Wind and snowbreaks are frequent, especially in stands of monostratified structure. The steepness of these mountains requires that the soil cover be always maintained, excluding a priori clear cutting of any size. Erosion, avalanches, and landslides are frequent, especially around Cortina and Longarone. Modern silviculture in this context seeks to be "nature oriented," i.e. to manage forests to get structures and functions similar to those of natural forests (Susmel 1980). Nevertheless, although the ecological and protective role of the forests in this region is primordial, their economic importance for local communities cannot be neglected. They are often communal forests, ruled by ancient customs or "regale," and contribute substantially to the income and pride of ownership of local people (Merlo, 1995).

 

Methods

AN OBJECTIVE OF MY WORK has been to quantify the consequences of unevenaged management on economic returns and ecological criteria, especially diversity. Recognizing the importance of both objectives in most settings, the goal is to measure the trade-off between income and diversity. To do this, it was necessary to develop methods to predict stand growth, simulate the effect of alternative management practices, and seek the best practice for a given set of objectives.

 

Growth Models

To FORECAST THE EFFECTS of different management practices in uneven-aged forest stands modern foresters use mathematical models. The purpose of such models is to simulate the growth of trees as they compete, die, and reproduce themselves over time. A growth simulator run on a computer can quickly mimic the evolution of a forest stand of trees that would take decades or centuries in the real world. In essence, the growth model allows the forester to bring the woods into the laboratory, and to experiment with them in a way that would be impossible in the wild (Holling et al., 1986).

Although growth models are abstractions, they capture the critical elements of the stand of trees, i.e. those that are directly relevant to management issues, and provide insights that could not be gotten in any other way. The introduction of modeling during the past 30 years has totally transformed the discipline of forest management, making it much more rigorous and subject to scientific inquiry. In the process, matters such as uneven-aged management, that seemed for a long time to be almost art forms, have become cod)fied and available in undergraduate textbooks (Buongiorno and Gilless, 1987).

The general form of growth models for uneven-aged stands can be expressed with the following equation:

 

 

where yt is a vector, a column of variables, each one being the number of trees per unit of land (say per ha? of a particular species and size, at a particular point in time, t. Therefore, y t is a summary description of the stand state at time t. This description has aufficient detail to model stand dynamics, to define meaningful criteria of stand diversity, and to assign accurate market values to stands and harvests.

The purpose of the equations in the growth model is to predict the stand state in the next period, t+1, given its current state at t. This is done in part with the matrix G. a table of numbers that measure the probabilities that a tree of a given species and size at t will be alive and of the same size, or alive and of the next higher size, at t+1.

The rest of the model consists of the column of variables It, in which each variable is the ingrowth of the trees of a particular species, that is the number of trees that enters the smallest measured size class between t and t+1.

In its simplest form the parameters of the growth model are independent of the stand state, and the model is linear (Usher 1969, Bruner and Moser 1973, Buongiorno and Michie 1980). Non linear forms complicate the management analysis, if optimal regimes are sought (Adams and Ek1974, Buongiorno et al. 1995), although they have little effect on the performance of simulations. Still, the gains obtained by recognizing non linearities are marginal in terms of forecasting accuracy, and probably do not justify the complication (tin and Buongiorno 1996).

Growth models of this kind can be developed from a variety of data sets. The simplest, assuming constant parameters and constant ingrowth can be calibrated knowing only (1) the state the forest would achieve after a very long time, and without exceptional disturbances, i.e. the climax state, and (2) the mortality rate (Houde and Ledoux 1995). However, it is useful to have additional data to estimate how the stand state affects ingrowth (Ingram and Buongiorno 1996). Indeed, much of the variation in stand dynamics arises from changes in ingrowth, rather than from changes in upgrowth rates. A good data set consists of a number of permanent plots observed at least twice, at intervals of a few years, with a tally of the trees by species and size, and a record of the trees cut and dead between the two measurements.

Once a growth model has been calibrated, its forecasting accuracy must be assessed. Ideally, this is done by applying the model to a set of data not used in model calibration, and comparing the stand states predicted by the model with those actually observed. However, such data are scarce, and they usually cover only a few years. To be useful in management, a growth model must be realistic over several decades, and even centuries. One test consists in comparing the asymptotic stand state predicted by the model, as time increases to infinity, with data from stands that are believed to be close to a climax state. For northern hardwoods in Wisconsin, we have used for this purpose data from the Menominee Indian Tribe forests, which still have some old growth stands that have had little disturbance for many decades (Lin et al., 1996a).

Often, however, one has to rely on less specific information regarding the species composition and stand structure of climax forests. For example, in the Southeastern coastal plain of the United States, the extensive ecological studies of Quarterman and Keever (1962), and Switzer et al. (1979) conclude that the natural climax of forests in the southeastern coastal plain is dominated by hardwoods. This gives credence to long-term forecasts obtained with the model of Lin et al. ( 1996b) for loblolly pine in the Southern United States (Figure 1). According to the model, without human intervention, pines would disappear in about three hundred years, and stands would be dominated by hardwoods.

 

Simulating management regimes

ONCE A GROWTH MODEL has been calibrated and tested, it can be used to predict the effect of different harvesting regimes. Uneven-aged management consists essentially of removing some of the trees, some of the time. How a stand will develop can then be predicted simply by introducing a harvest in the growth model (1):

 

where ht is the harvest vector. It is a column of variables, each one being equal to the number of trees of each species and size, cut at time t, per unit area. In general, It would also vary with the harvest: other things being equal, one would expect ingrowth to increase as more trees are removed.

Different rules may be followed to define the harvest ht. For example, it may be set as a fraction of the living trees, or it may be defined by a target residual stand. Trees above the target would be cut, while those below would remain. The harvest may also be defined by a diameter limit, whereby all trees above a certain size would be cut.

Table 1 shows the predicted effects of different management regimes on economic returns and ecological criteria on uneven-aged stands in the Italian Dolomites. All maintain at least 22 m2/ha of basal area, the minimum deemed necessary for forests of this region to keep adequate soil cover against erosion. If a dense diverse forest with many large trees were the goal, doing nothing or at most salvaging some mortality would give good results, apart from a slight decrease in species diversity due to the decline of secondary conifers. But the opportunity cost of doing nothing, in terms of timber income, would be very high compared to all other alternatives.

Instead, pursuing the current management method, set by Susmel's (1980) cultural model at 31 m of dominant height, would yield substantial income, at slightly higher species diversity, and about the same size diversity as doing nothing, though with lower basal area. Choosing a cultural model for a higher dominant height, which was being considered at the time of this study, would have little ecological impact, but a sign)ficant opportunity cost.

Applying a diameter-limit cut of 60 cm for conifers and 45 cm for beech (similar to the silvicultural guides of the Republic of Venice) could be attractive in some circumstances because it doubled income, relative to the cultural model. Species diversity was at least as good, but size diversity was much decreased because the policy removed the largest trees every 10 years.

Currently, there is much interest in the Veneto region to favor beech in forest stands to return to a more natural aspect of the forest. Interestingly, our simulations showed that a policy aimed at saving the beech, in conjunction with the cultural model, was counterproductive, leading to less beech and lower species diversity than would come from either the plain cultural model, or anyone of the diameter-limit policies (Table 1). Also unattractive was a policy perpetuating the current rate of cut: although it led to the highest size diversity, it produced also the lowest income (apart from doing nothing), and the lowest species diversity of all alternatives.

Forest managers in this region are also thinking of increasing the cutting cycle from 10 to 15 years, to reduce the impact of the high fixed cost incurred at every harvest. However, our simulations showed that, from an economic viewpoint, it would be better to shorten rather than lengthen the cutting cycle (Table 2). The economics were especially improved in that way for the most intensive diameter-limit cuts. The benefit of a longer cutting cycle would be to increase size diversity, though it would have no effect on species diversity.

Optimizing management regimes

SIMULATION IS A POWERFUL WAY of predicting the effects of different policies for uneven-aged stand management. However, there is an infinite number of possible policies to choose from and simulate. Ideally, one would like to be able to find systematically the best policy among all the possible ones. System optimization, the central theme of operations research, has been applied extensively by foresters for the past thirty years, first to even-aged management, and more recently to the uneven-aged case.

The growth model for a managed stand under harvest (2), can be readily embedded in an optimization model, by adding an objective function expressing the manager's objective, and a set of constraint. For example, if the management goal is to maintain a stand of highest possible diversity, while maintaining a sustainable forest, the model formulation would be:

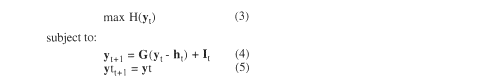
where H is a measure of the diversity of the forest stand. For example, Shannon's index (Magurran 1988) would give maximum diversity for a stand that had trees evenly distributed by species and size. Though these are simple measures of diversity, they determine to a large extent the total biological diversity of a forest stand (MacArthur and MacArthur 1961; Ambuel and Temple 1983). Equation (4) is the same as the growth equation (2). Equation (5) is the steady-state equation, which, as written, assumes that the cutting cycle is equal to the interval between t and t+1 that has been used to calibrate the growth model. The steady state equation implies that the growth just replaces the harvest, and therefore, harvest and stock can be maintained in perpetuity.

Mathematical procedures and related computer software are now available in popular spreadsheets to find the value of the harvest ht and of the stock yr that satisfy this system of equations. The solution is relatively simple if the model is linear in the variables, but it is tractable also in other cases, e.g. when the objective function is a highly non-linear function like in Shannon's index.

For example, we have solved this problem with data from northern hardwoods in Wisconsin, to find the harvest that would maximize the size diversity of an uneven-aged maple-birch stand in the steady state. The finding was extremely interesting: the best harvest was no harvest at all. Nature, by its natural growth and mortality process would result in an uneven-aged climax stand, sustainable forever, of maximum size diversity (Buongiorno et al., 1994). We found similar results for forests in the Jura mountains in France and in the Dolomites in Italy: no cut, or a light cut led to the highest diversity of species and size. However, this was not the case for the diversity of species in the South. There, as observed above, natural succession would tend to eliminate softwood species (Figure 1).

The optimization model can be changed in various ways to answer related interesting questions. For example, the objective function (3) can be changed by the present value of the harvests over an infinite horizon, net of all costs, including the cost of holding the growing stock, to find the uneven-aged stand structure and the harvest that would maximize income. In the case of the Jura mountains we found that the result would consist of a pure spruce stand. Beech and fir would be cut very young because they had lower unit prices. The largest spruces would be 40 cm and diameter, and all of them would be cut every 5 years, plus half of the spruce in the 35 cm size class.

This would yield a 6% real rate of return on the capital invested in growing stock, a handsome return considering that the real rate of return on government bonds in France during the past 20 years was less than 3% per year. The drawback, of course, is that the stand diversity would be very low. With only very young beech and fir, and with spruce no larger than 40 cm, stand diversity would be about half that of a stand of maximum sustainable diversity.

A better way, in most instances, to use the model is not to seek extreme managements that maximize either diversity or net present value, but to design compromise solutions. This can be done by maximizing returns, while keeping diversity above a minimum desired level. Or, maximizing diversity, subject to obtaining a specific financial return from the capital invested in trees. For example, Table 3 shows a steady-state prescription for uneven-aged stands in the French Jura that would maximize the minimum number of trees in any size and species class, while obtaining a real rate of return of 3% per year on the capital invested in the trees left after harvest. In this case, the stand would always have some trees of every species and size.

Such comparisons are useful, because they give quantitative measures of the trade-off between ecological objectives, such as diversity, and economic returns. In general, one would expect that increasing one objective comes necessarily at the cost of another, yet this is not always the case. For example, in our studies of northern hardwood stands, we found that diversity of tree size could be increased up to 90% of the maximum achievable (in Shannon's sense), while increasing financial returns. In that range, the two objectives are complementary, for the simple reason that income increases as the size of trees in the stands increases. But this is true only up to a point, beyond 90%, one must give up very much in income to gain little in diversity (Figure 2).

 

Dealing with risk and landscape diversity

The methods described so far have used deterministic models, at stand level. Yet, biological and economic variables are in large part random. Moreover, the analysis must be expanded to a landscape level. Each stage of stand growth provides critical habitats for some plants and animals, and paying attention to any particular stage only, including old growth, is misdirected for the sake of biodiversity (Hansen et al. 1991, Oliver 1992).

Markov models have proved useful in this context. They classify all possible stand conditions in a landscape into a finite number of states. The core of the method then is a table giving the probabilities that a stand will be in different states in the next period of observation, given its beginning state. Management has simply the effect of changing the beginning state. Application of the method in forestry was pioneered by Hool (1966), and Lembersky and Johnson (1975). It was later applied to uneven-aged management by Kaya and Buongiorno (1980) and Lu (1992), but mostly to study the effects risk on economic returns.

More recently, we have applied markovian models to predict the diversity of forest stands and landscapes in managed forests (tin and Buongiorno 1996). Applied to the Wisconsin northern hardwoods, the methods recognize the randomness of biological growth and timber prices. Transition probabilities between stand states are obtained by simulation, still with model (2), but with the addition of a random term estimated from the plot data. Shannon's index measures tree and species diversity in each stand state. The distribution of stand states throughout the sample plots measures landscape diversity. Then, the landscape is most diverse when plots are evenly distributed among stand states. It is least diverse when all plots are in the same state.

The results have shown that stands in an old growth state would dominate the landscape if the forest were undisturbed: they would have many large shade tolerant trees. Landscape diversity increases with the frequency of natural catastrophes (Table 4), unless catastrophes are extremely frequent, in which case diversity decreases, a result also found by Frelich and Lorimer (1991). Continuation of the current management policy would double the landscape diversity relative to an unmanaged forest, but the proportion of old growth stands would be reduced by 75%, size diversity would be 1/3 lower, while species diversity would be about the same (Table 5).

Applying the Markovian models to obtain best policies under risk showed that income (net present value of the return to the land, or soil rent), could be quintupled, without affecting landscape diversity, but at the cost of reducing diversity of tree species and size (Table 5). Seeking maximum species diversity requires harvesting, it lowers landscape diversity and leads to about the same size diversity, reducing income by two thirds relative to the maximum, though doubling it relative to the current policy. Maximum tree size diversity could be achieved by letting nature take its course, giving up most income, and having a landscape half as diverse as that obtained by continuing the current policy. The method was also applied to find compromise policies that maximized income, while keeping diversity of tree species or size above a critical level. The results suggest that it costs less to increase species than size diversity because cutting large trees tends to increase openings and species diversity.

 

Conclusions

UNEVEN-AGED MANAGEMENT can be observed in many forest types throughout the world. Some of the oldest managed forests have been managed that way. Like Moliere's Monsieur Jourdain who spoke prose without knowing that he did, many communities, especially in the mountains of Europe, have managed their forests by the uneven-aged principles, whether they and their great-grand fathers knew it or not.

With the growing interest for so-called natural regimes in Europe and North America, it is worth noting that uneven-aged forests have often been the norm in undisturbed stands, in many forest types, even where it is generally not thought to be so. For example, the traditional view of the forests of Finland is that they are even-aged. Yet, Lahde, E. et al. (1991) believe that "this is based on the common practice of determining the age of only the dominant trees and to accept a wide age variation in the concept of even-agedness," instead they found that "in the 1920's, the majority of advanced virgin forests [in Finland] were mixed stands with an all-sized structure." We had a similar experience with the Forest Inventory and Analysis data of the Southwestern United States. Although the loblolly-pine type is typically thought of being monospecific and even-aged, we found many plots with mixed-species of all-sized stands, with an abundance of small trees and a diminishing number of trees with increasing stem diameter, i.e. the typical unevenaged structure.

The information available seems to be enough in many managed forests around the world to develop quantitative models of forest growth under unevenaged silviculture. Although long-term observations of forest growth are hard to get, much can be done with just two measurements, taken a decade or so apart, from a cross-section of sample plots. A tally of trees by species and size class at the beginning and end of the interval, plus a record of the trees that have been cut and those that have died, is enough to build such a growth model. This kind of data is often available from ordinary management records. If mortality data do not exist, they can often be guessed from experience. Such "soft" data may lack formal rigor, but they will produce a practical model in short order. It is then relatively easy to check if the model mimics growth reasonably well. I believe that it is much better to have an eclectic model to help management than no model at all, or to wait decades for the perfect data and perfect model (which do not exist anyway).

Management decisions have to be made now and they must be based on rigorous thinking, with all available information. Part of that information can be condensed efficiently in a model well grounded on field data. As discussed above, the model can then be applied in simulations to judge the effects of many management regimes. Or, it can be part of optimizations to define the best management alternative. The results have shown some very interesting patterns. One is the tendency of natural processes to seek equilibrium states of maximum diversity. For example, we have observed that maximum diversity of tree size in northern hardwoods would be achieved by not cutting any tree. Also, storms and other catastrophic disturbances led to landscapes of higher diversity.

Another result of practical sign)ficance is that economic goals are not always necessarily in conflict with ecological objectives. For example, up to a tree size diversity of about 90% (relative to the sustainable maximum), there is no conflict but rather complementarily between economics and tree size diversity. To get a higher soil rent, one must also increase stand diversity. This makes full sense: more trees of large size increase both diversity and economic returns, up to the point where the capital holding cost becomes excessive relative to the returns, in which case soil rent drops drastically.

In this approach, the underlying principle is that the value of some forest management objectives cannot be measured with current economic methodology. They may never be. The value of a species, or the value of a sunset on the Grand Canyon, are more ethical, philosophical, and religious issues than economic. The examples we gave have tried to measure only the opportunity cost of management alternatives, i.e. how much it would cost in terms of measurable market goods like timber, to protect a species, or to increase the diversity of a forest stand. Such opportunity costs can be obtained readily with current methods. And, despite their clear limitations they are critical in decision making. The rest depends on the forester's wisdom, of which plenty should be used. Wisdom means recognizing the very limited knowledge we have, regarding biological processes and future human needs. In face of such uncertainty, drastic irreversible decisions should be always be avoided. In terms of methods, the formalization of these irreversibilities, and their inclusion in decision-making is a natural next step for future research.

References

Adams, D.M., and A.R. Ek. 1974. Optimizing the management of uneven-aged forest stands. Canadian Journal of Forestry Resources 4:274-287.

Ambuel, B., and S.A. Temple. 1983. Area-dependent changes in the bird communities and vegetation of Southern Wisconsin forests. Ecology 64(5): 1057- 1068.

 

Ammer, O. 1994. Let's take a walk in the woods. Naturopa 75:8.

Bare, B.B., and Daniel Opalach. 1987. Optimizing species composition in unevenaged forest stands. Forest Science 33(4):958-970.

Bliss, J.C., and A.J. Martin. 1989. Identifying NIPF management motivations with qualitative method. Forest Science 35(2):601-602.

Bruner, H.D., and J.W. Moser. 1973. A Markov chain approach to the prediction of diameter distributions in uneven-aged forest stands. Canadian Journal of Forestr Resources 3:409:417.

 

Buongiorno, J., and H.-C. Lu. 1990. Economic stocking and cutting-cycle in a regulated selection forest. Foest Ecology Management 32:203-216.

Buongiorno, J., and J.K. Gilless. 1987. Forest management and economics, a primer in quantitative methods. MacMillan.

Buongiorno, J., and B. Michie. 1980. A matrix model of uneven-aged forest management. Forest Science 26(4):609-625.

Buongiorno, J., S. Dahir, H.C. Lu, and C.R. Lin. 1994. Tree size diversity and economic returns in uneven-aged forest stands. Forest Science 40(1):83-103.

Buongiorno, J., Peyron, J., Houllier, F. and Bruciamacchie, M., 1995. Growth and management of mixed-species, uneven-aged forests in the French Jura: Implications for economic returns and tree diversity. Forest Science, 41(3):397429.

 

Ciancio, O., and S. Nocentini. 1994. Gurnaud's control method and silviculture on natural basis: a forest management and silvicultural question. L'Italia Forestale e Montana 49(4):336-356.

 

Daniel, Th. W., J.A. Helms, and F.S. Baker. 1979. Principles of Silviculture. 2nd ed. McGraw-Hill, New York.

 

Farrar, R.M. 1981. Regulation of uneven-aged loblolly-shortleaf pine forests. In Baronet, J.P. (ed.), Proceedings of the First Biennial Southern Silvicultural Research Conference, USDA Forest Service General Technical Report. S0-34.

Frelich, L.L, and C.G. Lorimer. 1991. A simulation of landscape-level stand dynamics in the northern hardwood region. Journal of Ecology 79:223-233.

Guldin, J.M., and J.B. Baker. 1988. Yield comparisons from even-aged and uneven-aged loblolly-shortleaf pine stands. Southern Journal of Applied Forestry 12:107-114.

Gurnaud, A. 1886. La sylviculture fran,caise et la methode du controle. Besan,con. 121p.
Haight, R.G. 1985. A comparison of dynamic and static economic models of uneven-aged stand management. Forest Science 31 :957-974.

Hansen, A.M., T.A. Spies, FlJ. Swanson, and J.L. Ohmann. 1991. Conserving biodiversity in managed forests: lessons from natural forests. BioScience 41 (6):382-292.

Holling, C.S., G.B. Dantzig, and C. Winkler. 1986. Determining optimal policies for ecosystems. in Kallio et al., Eds. Systems Analysis in Forestry and Forest Industries. TIMS Studies in the Management Sciences 21:453-473.

Hotvedt, J,E., Y.F. Abernethy, and R.M. Farrar, Jr. 1989. Optimum management regimes for uneven-aged loblolly-shortleaf pine stands managed under the selection system in the West Gulf region. Southern Journal of Applied Forestry 13(3):117-122.

Houde, L., and H. Ledoux. 1995. Modelization in natural forests: stand stability. Bois etforets des tropiques 245:28-31.

Hool, J.N. 1966. A dynamic programming-Markov chain approach to forest production control. Forest Science Monograph 12.

Ingram, C.D., and J. Buongiorno. 1996. Income and diversity tradeoffs from management of mixedl lowland dipterocarps in Malaysia. Journal of Tropical Forest Science (forthcoming).

 

Kaya, I., and J. Buongiorno. 1980. Economic harvesting of uneven-aged northern hardwood stands under risk: A markovian decision model. Forest Science 33(4):889-907.

Lahde, E., O. Laiho, Y. Norokorpi, and T. Saksa. 1991. The structure of advanced virgin forests in Finland. Scandinavian Journal of Forest Resources 6:527-537.

 

Lembersky, M.R., and K.N. Johnson. 1975. Optimal policies for managed stands: an infinite horizon Markov chain decision process approach. Forest Science 21(2): 109-122.

Lin, C.R., and J. Buongiorno. 1996. Fixed vs. variable-parameter matrix models of forest growth: the case of maple-birch forests. Department of Forestry, University of Wisconsin, Madison.

Lin, C.R., J. Buongiorno, and M. Vasievich. 1996a. A multi-species, density dependent matrix growth model to predict tree diversity and income in northern hardwood stands. Ecological Modeling (forthcoming).

Lin, C.R., J. Buongiorno, J. Prestemon, and K. Skog. 1996b. A growth model for uneven-aged loblolly pine stands, with simulations and management implications. Department of Forestry, University of Wisconsin, Madison. Liocourt, F. De. 1901.

 

Lin, C.R., and J. Buongiorno. 1996. Tree divesity, landscape diversity, and economics of maple-birch forests. Part I: Implications of a Markov-chain model. Part II: Optimization with a Markov decision process model. Department of Forestry, University of Wisconsin, Madison.

Lu., H.C. 1992. Economic management of Wisconsin's northern hardwood forest stands: A mixed-species model. PhD Dissertation, University of Wisconsin, Madison.

 

Lu, H.-C., and J. Buongiorno. 1993. Long- and short-term effects of alternative cutting regimes on economic returns and ecological diversity in mixed-species forests. Forest Ecological Management 58: 173- 192.

Magurran, A.E., 1988. Ecological diversity and its measurement. Princeton University Press, Princeton, N. J., 179 pp.

MacArthur, R.H. and J.W. MacArthur. 1961. On bird diversity. Ecology 42(3):594-600.

Merlo, M., 1995. Common property forest management in northern Italy: a historical and socio-economic profile. Unasylva 46:58-63.

Murphy, P.A., and M.G. Shelton. 1994. Growth of loblolly pine stands after the first five years of uneven-aged silviculture using single-tree selection. Southern Journal of Applied Forestry 18(3):128-132.

Niese, J.N., and T.F. Strong. 1992. Economic and tree diversity trade-offs in managed northern hardwoods. Canadian Journal of Forest Resources 22:1807-1813.

 

Oliver, C.D. 1992. A landscape approach to achieving and maintaining biodiversity and economic productivity. Journal of Forestry 90(9):20-25.

Quarterman, E., and C. Keever. 1962. Southern mixed hardwood forest: Climax in the southeastern coastal plain, U.S.A. Ecological Monographs 32(2):167-185.

Schaeffer, A., A. Gazin, and A. D'Alverny. 1930. Sapinieres; le jardinage par contenance (methode du controle par les courbes). Presse Universitaire de France, Paris. 100p.

Susmel, L., 1980. Normalizzazione delle foreste alpine. Liviana, Padova. 437 pp.

Switzer, G.L., M.G. Shelton, and L.E. Nelson. 1979. Successional development of the forest floor and soil surface on upland sites of the East Gulf Coast Plain. Ecology 60(6): 1162-1171.

Usher, M.B. 1969 a. A matrix approach to the management of renewable resources, with special references to selection forests - two extensions. Journal of Applied Ecology 6:347-348.

Usher, M.B. 1969 b. A matrix model for forest management. Biometrics 25: 309315.

 

Volin, V., and J. Buongiorno. 1996. Effects of alternative management regimes on forest stand structure, species composition, and income: a model for the Italian Dolomites. Forest Ecology and Management (forthcoming).

Williston, H.L. 1978. Uneven-aged management in the loblolly-shortleaf pine type. Southern Journal of Applied Forestry 2:78-82.

 

 

---

Table 1. Effects of management policy on income and diversity of uneven-aged forest stands in the Dolomites.

 

Policy	NPV (1000 L/ha)	Species diversity	Size diversity
Harvesting only the dead trees	-281	95	103
Approximating the cultural model	2,679	96	102
Diameter limit = 70 conifers, 50 beech (cm)	2,144	96	103
Diameter limit = 60 conifers, 45 beech (cm)	5,763	97	96
Saving the beech	2,290	94	103
Perpetuating the current cut rate	1,788	94	105

 

Note: NPV = net present value of income over 10 years. Diversity = averages of
Shannon's indices over 10 years observed every 5 years, just before harvest. Cutting cycle = 10 years (Volin and Buongiorno, 1996).
 

Table 2. Effects of cutting cycle on income and diversity of unevenaged forest stands in the Dolomites.

 

Policy	Cutting Cycle (year)	NPV (1,000 L/ha)	Species diversity	Size diversity
Approximating the cultural model	5	2,847	96	101
	10	2,679	96	102
	15	2,314	96	103
Diameter limit = 60 conifers, 45 beech (cm)	5	6,503	97	93
	10	5,763	97	96
	15	4,886	97	99

 

 

Note: NPV = net present value of income over 120 years. Diversity = averages of Shannon's indices over 120 years observed every 5 years, just before harvest. Cutting cycle = 10 years (Volin and Buongiorno, 1996).
 

Table 3: Steady state that maximizes diversity, with an internal rate of return on growing stock of 3% per year,
in forests of the Jura.

 

Diameter  (cm)	Firs/ha		Spruce/ha		Beech/ha
	Stock	cut/5 yr.	Stock	cut/5 yr	Stock	cut/5 yr
20	11	6	52	0	13	0
25	5	0	45	0	7	5
30	4	0	6	3	3	0
35	3	0	16	13	2	0
40	3	0	3	0	2	0
45	3	0	3	0	2	0
50	2	0	2	0	2	0
55	2	0	2	0	2	0
60+	3	1	3	1	3	1

 

Source: Buongiorno et al. (1995).
 

 

Table 4: Effects of catastrophes on forest diversity.

 

Diversity	Current Forest	Steady state forest
		Without catastrophe	With catastrophes
Landscape	3.63	0.94	1.52
Tree species	0.75	0.86	0.86
Tree size	0.46	0.98	0.92

 

Note: Numbers are Shannon's indices of diversity (Lin and Buongiorno 1996).
 

 

Table 5. Effects of alternative management policies on diversity.

 

		Current	Maximizing
			Income	Diversity
				Species	Size
Diversity	Landscape	3.33	3.32	2.35	0.91
	Tree species	0.81	0.78	1.04	0.84
	Tree size	0.60	0.55	0.60	0.98
Income ($/a)  114		114	637	247	25

 

Note: Diversity = Shannon's index. Income = net present value of timber harvest, over an infinite horizon (Lin and Buongiorno 1966).
 

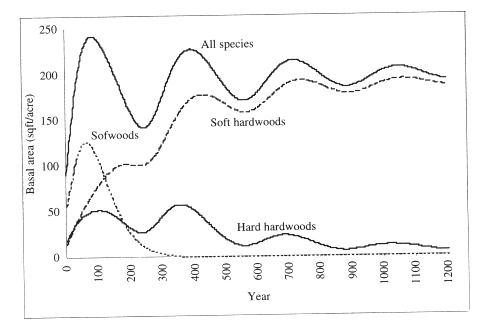
Figure 1. Long-term growth of an undisturbed loblolly pine stand in the southeast on a good site (Lin et al., 1996b).
 

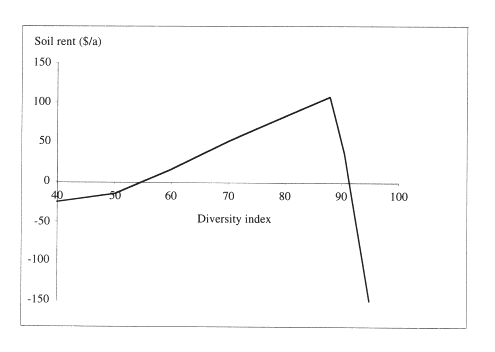
Figure 2. Highest soil rent obtainable at different levels of tree size diversity in maple-birch forests (Buongiorno et al. 1994).

Acknowledgments

THE MATERIAL OF THIS LECTURE is based in part on research on uneven-aged management in several countries that I have done over many years with several colleagues. Among former graduate students at the University of Wisconsin I would like to acknowledge the contribution of Bruce Michie, Ismail Kaya, Hsien-Chi Lu, Ching-Rong Lin, Denise Ingram, Valeria Volin, and Paola Virgilietti. I am also grateful for the collaboration of JeanLuc Peyron of the ENGREF in Nancy, France, Maurizio Merlo of the University of Padua, Italy, Birger Solberg of the European Forest Institute, Joensuu, Finland, the late Hyung Kang and Mike Vasievich of the USDA Forest Service, North-Central Forest Experimentation, and Ken Skog of the Forest Products Laboratory. The research leading to this paper was supported by grants from the McIntire-Stennis Program, USDA Forest Service NC Station and Forest Products Laboratory, European Forest Institute, the University-Industry Research Program and the School of Natural Resources at the University of Wisconsin, Madison.